压力反馈调速器的分析

对于压力反馈调速器元件的名称，可参考图4-8a。

这是一个用来表示工作原理的小信号分析装置，为了仔 细分析这一装置，从三个单独的部分进行分析。即：

基本调速器

飞块弹簧质量系统 弹簧驱动器

此外，采用了一些简化假设，即

(a) 摩擦力的影响忽略不计，

(b) 液压油的可压缩性忽略不计，

(c) 小孔特性被线性化(对于微量变化)。

(d) 导向阀的滑移力可忽略不计。

下面分别讲基本调速器和阻尼调速器的运动方程式。 (a) 基本调速器

在导向阀匕，力的平衡与简单机械调速器相同，只不过 在导向阀底面积五上附加了反馈压力pr,    于 是 导 向 阀 上 力 的平衡为：

飞块力Fw+   反 馈 力Ff=    弹 簧 力F                       (19)

将飞块弹簧质量系统的粘滞摩擦和质量一加速效应暂时 撇开，则

Fw=mo!2·q/p ·r

式 中o%  为发动机转速① 。在松弛耦合的条件下由弹性 驱动的飞块系统的转速。其反馈力Ff 为 ：

Ff=hPf

在现代调速器中，调速弹簧的绕制，要使它的力和压缩 距离之间有平方关系，从而与飞块的转速和离心力之间的平 方关系相匹配 。于是在整个转速范围内获得恒定的灵敏度 。 这样在整个工作范围内的弹簧力为：

F=K(X-α)²

同样由于比例反馈，给定速度随调速弹簧输出值y 而 变 更，即：

X=K         w₁-φy

式 中Ki0i    为给定速度， φ为反馈系数， 由此可得： F 。=K(Ki①;     一φy-x)²

现在假定参数条件有微小的变动，并且使用算子D ,    则

飞块力变为：

8Fw=Kδ06-R8x                                           (20) 

R=m(0%q/p)²

可见与机械调速器一萍 。反馈力

δFf=δp

8Fs=β(K,80,-ψ8y-8x) 式中： β=2K(Ki0;-φ?-x),度。(21)

为作用点上的弹簧刚

当给定速度为但定时，8co;=0   弹 簧 力 8Fg 为：

8Fg=-β(φδy+δx)                                          (22) 将式(20)(21)和(22)代入力的平衡方程式(19)得出：

K,δo+(β-R)8x+hδpr+8φδy=0                                         (23)

动力活塞的运动，可以从简单的流量一位移关系式(13)

求得：

于是反馈流量平衡式为：

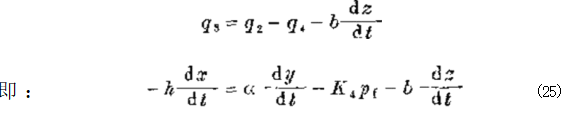
式中：K₄——  线性化节流小孔系数。 在补偿活塞上力的平衡为

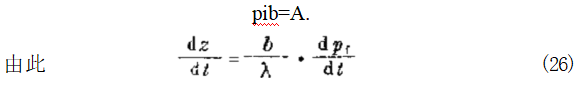
对于微量变化，关系式(25)变为：

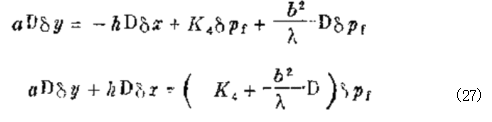
消去 δx , δpf      并重新整理得到

若 φ ≠0(降速)

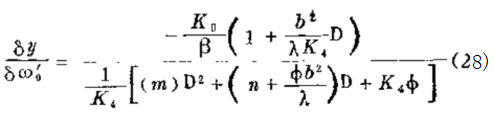
若 φ = 0 ( 同 步 )

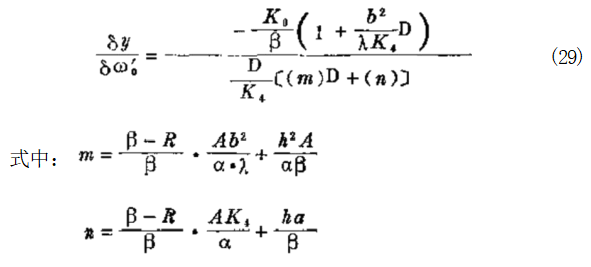
应注意的是： 降速调速器基本上是同阻尼的二阶响应和 在分子中的稳定相位超前项成适当比例， 由于1/D 项 的 原 因，同步调速器基本上是一个积分调节器。

液力反馈通路中的可调节流阀，实际上起变更K4  值 的 作用。关闭节流阀，K4   值降低，从而增大积分时间常数和 增大相位超前时间常数，这样来减慢和稳定其响应。

在降速情况下，稳态增益为：

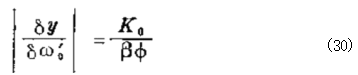
如果加以归一化，使用参考值y 和 o%, 使上式变为无 因次式

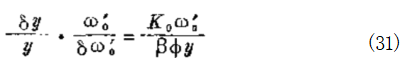
这是一个无因次的增益，它等于速度降的倒数，于是

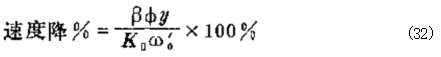
例如对于4%的速度降 ，增益K₀o%/βφy=25

这些方程描述了基本调速器的作用。然而在调速器内，

有两个重要因素干扰着整个响应，飞铁弹簧一质量系统及弹 簧驱动器。

为了论述清楚，我们稍作变更，并假设上述两类元件可 以分开叙述，则对于飞铁系统，可以应用一个二阶动态阻尼 项，简化增益式为：

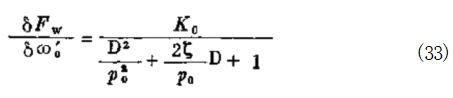
式中： p 。——飞铁克服与调速弹簧作用力的自然振荡频率，

典型为25Hz;

t ——导向阀等的运动粘滞阻尼系数，包括节流小孔 系数Kg 在反馈中对导向的影响。

另外 ，弹簧驱动器包括一套飞铁和托架等组成的惯性 体，这套惯性体通过弹簧耦联到驱动轴上。弹簧驱动器的运 动件之间有粘滞阻尼 ，很容易推导出这类装置的传递函数 为：

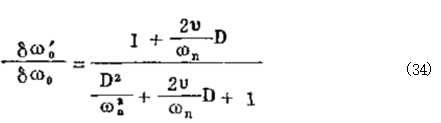
式中：o,——  调速器的实际输入速度；

①n——转动头与弹簧驱动器的自然振动频率；

v—--  弹簧驱动器中的粘滞阻尼系数。

于是在降速工作情况下，调速器的总传递函数为：

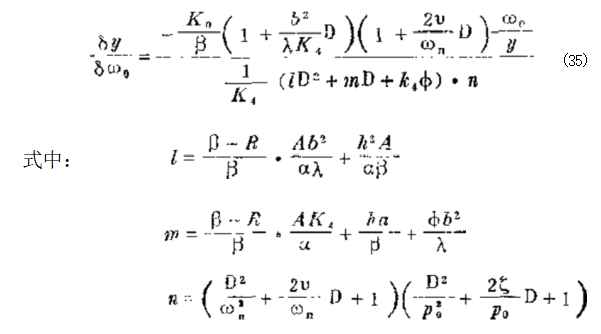
式中： φ ——速度降(可调)变动；

K ₄—      稳定性与晌应(可调)变动； λ——弹簧变化。

变动①n可以使调速器与发动机相匹配。 (b) 阻尼调速器

对于阻尼调速器，参看图4-3(b)  中各参数可写出与基本 调速器相似的方程式：

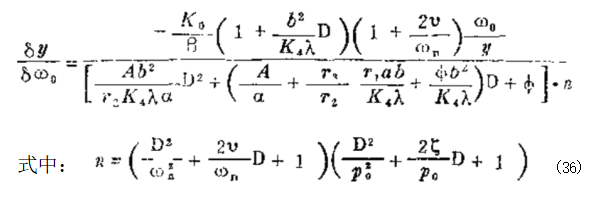
可以看出，这是一个稍为复杂的表达式，式中 K₄  和 r₁   为调节参数，它们对稳定性和响应有类似的影响，而参数φ

为可调速度降。

两种调速器具有类似的性能，均应用很广。