典型调速器性能参数

假定调速器输出功为20J,  转速1200r/min,   速 度 降 4 % 以及单向反馈节流阀开启。

空载至满载动力活塞行程15mm

0o … … … … … … … … … 125Eed/s

A…                      e        1535×10-9m²

b         …   m              …201×10       ³m²

a…               re    k     127×10-5m²

h…   ……                        71× 10-⁰m²

Ps …     设输出功20J             … … …1.0MN/m²

β ……转速调在1200r/min        2600N/m

λ ……选择一取为…       …350  N/m

m …    2×0.061                         … …0. 122kg

po              ……        20mm

q …             …                                     10mm

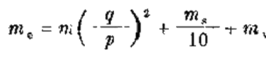“ mg/10    对平方律弹簧

Ke=2m(Oég/pr(r-p)                     …0.3kg ·n/s

R=m(0g/p)² …                       … … ·484N/m

K. … …  难于计算，接近于……0.05 × 10-8m⁵/s

… … 对于小开度 …    ……0.1 m²/s

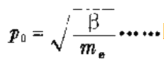即在开启点…168rad/s(26.75Hz)

——飞铁系统的阻尼系数，为1.0左右，设由液力

反馈系统中导向阀下部的阻尼孔决定。

On    … 选定为4 Hz     … … …25rad/s

U … …弹簧驱动器阻尼系数，约为1.0 于是调速器的总传递函数的典型式为：

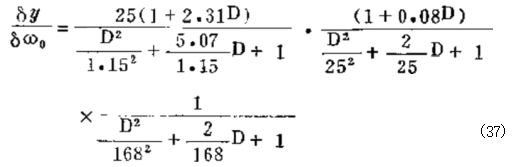
注意在这个简化的传递函数中，含有三个二阶滞后项，其分 割点为1.15rad/s,25rad/s        以及168rad/s,     而在液压伺服 机构中的相位超前项的分割点为1/2.31cad/s,  而 弹 簧 内 的 分割点为1/0.08rad/s。

在弹簧驱动器中并未真正需要相位超前项，它之所以出 现，是因为弹簧驱动器转子顶部受到的阻尼与转子驱动力成 正比，而理想情况下转子顶部受到的阻尼是相对地面而言 的。可惜的是，对容许尺寸的实际机构来说，理想状况不容 易达到。

从这个“简单 ”模型的构成来看，值得注意的是要经常 向调速器制造厂提出调速器的“时间常数 ”的要求。而“简 单 ”模型要回答“时间常数 ”这样的问题，其论据是不充足 的。调速器响应的唯一简维的指标是，转速大档位变化时的 过渡时间。转速大档位变化时，导向阀全开，导向阀全开只要 很短的时间，动力活塞则以最高速度移动。典型的现代调速

器的过渡时间为0.1s。 下面讲频率响应。

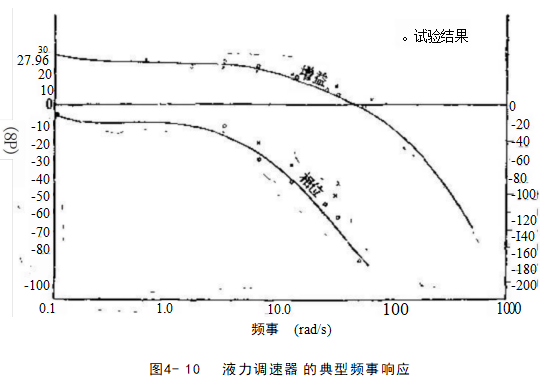
根据选定的典型事例，得到的增益和相位曲线如图4-10 所示，为便于比较，一些有关的试验结果，用不同的标点同 时绘在图上。实际上尽管有很多次要因素影晌着调速器的实 际效能，调速器的结构在细节上也很不相同，但从图中看出 几种试验结果还是大体相符的。

这些曲线着重表明了现代液力调速器的主要特点和性 能，希望大家能对其运行性能有一些了解。

参看图4-10,可以看到，由于液力伺服机构具有相位滞 后一超前补偿，增益在低频区略有衰减。相频曲线在中频区 稍有回升以利系统稳定(最为重要),而在高频区，增益曲 线则迅速跌落。

注意，相位滞后一超前补偿通常应用于调节器中可以提 高稳态精度，但是降低了中频区的灵敏度。另一方面，伺服机构通常利用相位超前一滞后补偿以便在尽可能宽的频带内 获得一根平坦连贯的闭坏增益响应曲线。

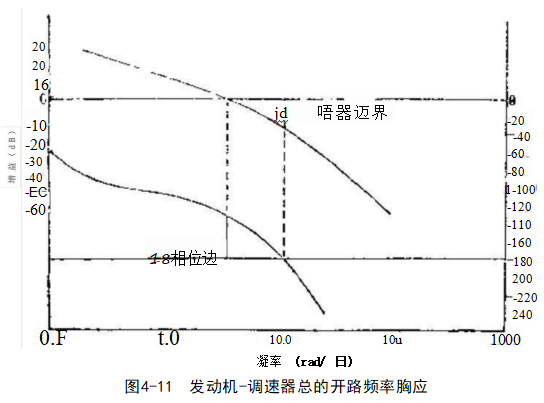
如果相位稳定边界降低，估计是因为系统内部间隙增 大，或调速器中润滑油的温度过低(冷起动稳定性是个常见 间题)所致；另一方面，由于调速器和发动机之间的杠杆比 不正确，或调速器中出现气穴，会使增益上升。于是可以看 到，组合装置将会在约1Hz 处振荡，这是多数发动机的 典型“猎振”频率*。

“猎振 ”是自动控制系统中的一种不希望出现的无规则尿荡，此时受

控变量在期望值的两这摆动— 一校注。

假知我们将液力同服助推调速器与简单机被调速器进行 对照，简单机横词速器飞铁总重2 kg, 旋转平径50mm, 那 么在1200x/min  下运转时，常用的数据为；

①;= 12Grcd/s;

g/p =1;

m=2    kg 总重； n 。=5000g

p=50mm;

y= 15mm  行程 速 度 降 = 4 %

为与液力调速器 作直接比较；

重量比R=m²1q/p)²=31752N/m

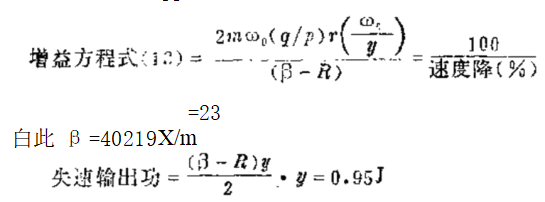
于是，按方程式(1í)机械调速器的传递函数变为： δx/80 。=-211680/(5D²+fD÷ 8467)

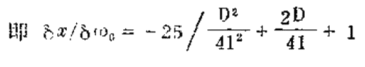
假定f 这样取，位总阻尼为1.0。

为了比较，选择了一个增益较高的情况(转速降不用较 逼真 的8%,而用4%),要求调速弹簧具有很大 的 刚度。

白此假设的弹筑一质量系统的自振频率是非常高的。

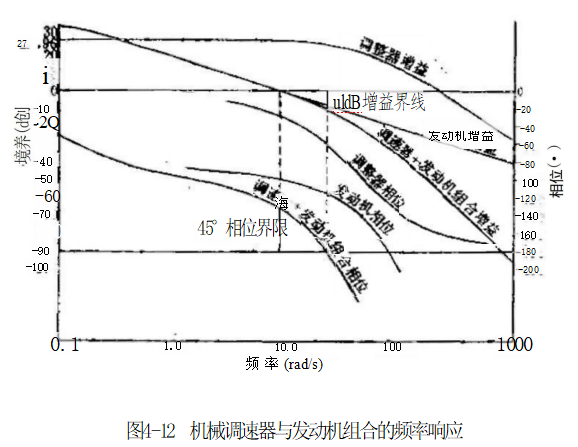
图4-12所示的发动机频率晌应由线，指出了充分稳定的 界线，不过，由于在低频区不无相位滞后一超前带来的增益衰减，故增益稳定界限小于液力调速器。

在选定的任意情况下，总的控制环路“猎振 ”频率稍微 偏高。

液力调速器与简单机械调速器的主要差别在于推动供油 齿条的有效输出功不同。使用“平均力x 行程 ”这个简单定 义作指标，可以看到，对机械调速器不到1J,   而对于液力 调速器，需要的有效功最高可达350J。

下面讲瞬态响应。

所谓瞬态响应，是指发动机负荷变化时，速度出现的瞬 时偏移。

为了计算调速发动机的瞬态响应，必须求出发动机一调 速器组合装置控制闭环的传递函数。这要求解一个七阶以上 的微分方程，于是就需要有一台计算机。由于所用设备中存 在的非线性和局限性，计算出的响应必然很不准确，其结果 是徒劳无用的。

对于这一课题已经做了大量理论性的研究工作，但推导 出的一些模型对日常使用来说显得过分复杂。

为了估价瞬态性能，制造厂用实验与经验相结合的办 法，对常规要求来说，可以取得足够的精度。不过要进一步 对这一性能进行检测和优化，终究还得在实验台上完成。

一般不能一次就把全负荷(100%负荷)施加给涡轮增压 发动机，而又不使其转速急剧下降或立即停机。因此，瞬态 试验应从零负荷开始，逐步施加部分负荷，以至到达预定标 准负荷范围内。英国工业标准5514(国际标准3046)中规定 了商用瞬态响应的验收性能。

对瞬态性能的佔价，主要依靠常识性的经验方法。

(a) 如果一台发动机具有50%/s  的加速率，而调速器从

空载到满载的过渡时间是0.1s,  显然，发动机负荷变化100% 时 ，将导致瞬时速度至少变化50 × 0. 1=5% 。 实 际上 ， 由 于系统中各种滞后因素的影响，并由于调速器在0.1s 的 过 渡时间内，只能渐进地改变供油的速率，所以，瞬时速度的 变化至少是8 %左右。

(b)  更精确的瞬态响应偏差，可用下式计算：

(加速率%)毒 × 调速器滞后+加速率% × 发动机滞后

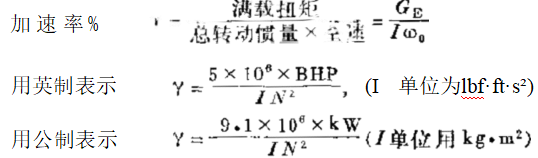
注意，在欧洲，有时用宜径的乎方项来表示I,所 以 在 Y的式子中必须乘以4。

下面讲调速器滞后。

从本文中所用调速器为例，该调速器能以1500r/min   速 度运转 ，具有10,20或34J的输出功，其灵敏度随标准飞块  (或小飞块)的重量而变 。该调速器滞后有四个因素。

f=1 。0  对输出功为10J 的 调 速 器 或 f= 1 . 1     对输出功为20,34J  的调速器

(由于使用较大的动力活塞，速度变慢)

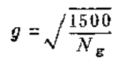
式中： Ng——   调速器额定驱动转速(例如由发动机通过齿

轮驱动)。

h= 0 .75      (对于标准飞块)或 h= 1.0     (对于小飞块)

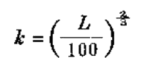
式中：L-—       负荷变化的百分率。 下面讲发动机滞后。

不同型式发动机的滞后变化。假如 N= 1200r/min        (发动机转速)

= 16 (气缸数)

8 = 4 ( 四 行 程 发 动 机 )或 s=2       (二行程发动机)

则，对于柴油机，根据方程式(6)得出：

发动机滞后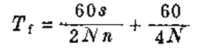

于是，降时速度偏离可估计为：

n%=fog·k·E√ Y+YTp

对已举例子 ，负荷变化50%,加速率Y=50%/s   其瞬态

响应偏差大概为：

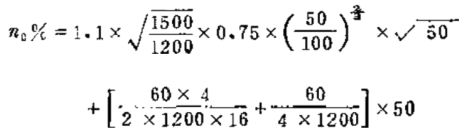
=4.102+0.9375

也就是说 ， 负荷变化50%,瞬态响应偏差约为5%,负 荷变化100%,瞬态响应偏差约为7.5% 。这样的特性是符合正 常要求的。

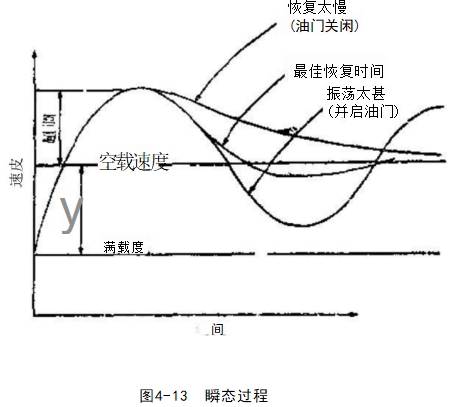
图4-13表示典型瞬态响应情况及调整油门螺钉对响应的 影响。