控制算法的介绍

动态特性的描述

在这里我们要重点研究一下控制理论，它是用计算机对机械 进行控制时的理论基础。

作为用计算机控制的机械，有操作手、人造卫星、飞机等，它们 的动态特性都是可以用微分方程来描述的。和用控制器可以直接 操作的量(操作量，控制输入),有发生在关节上的力矩，火箭发动 机的推力，机翼的形状等。显然，利用这些控制量可以控制操作手 的关节角、人造卫星的轨道、飞机的位置和姿态的期望状态：当控 制对象为机械时，上述输人-输出关系可以用微分方程式描述。不 过，描述输入与输出关系的微分方程式，只是近似地反映了系统的 动态特性。越要提高近似精度，微分方程就会变得越复杂，而且计 算时间也会越长，这样反而容易忽略问题的本质。因此，从实现满 足运动动态特性要求出发，微分方程总是具有某种近似程度的，从 而可以选择具有简单形式的微分方程式。

例如，对于图3.4所示的由两个联杆构成的简单联杆机构，试 求其运动方程式。这个例子虽然简单，却包含了后面将要讨论的 一些重要观点，因此它具有典型性。

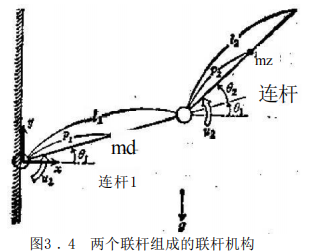
这个联杆机构，由质量为 m, 绕重心的惯性矩为 J 和长度为4(i=1,2) 的两个联杆组成，并且设它的运动被约束在垂直面内。 各关节只能作旋转运动，旋转角θ:的选取如图所示。 各个关节 上安装有执行器，当产生力矩 时，联杆便作旋转运动。因为重 心的位置(x₁,yi),(x₂,y₂) 分别为 (x₁sy₁)=(picosθ₁,prsinθ₁), (x₂,y₂)==(Icosθ₁+p₁cos(θ₁+θ₂),l sinθ₁+p₂sin(θ₁+θ₂)), 所以重心的速度为(龙，y) 一 (一pθ₁sinθ,pθ₁cosθ₁),(*,9₂) =(-L0 sinθ₁一p₂(₁+O₂)sin(θ₁+θ₂),hθ₁cosθ₁ 十 p₂(O₁+ θ₂)cos(θ₁+θ₂)). 因此，动能T 为：

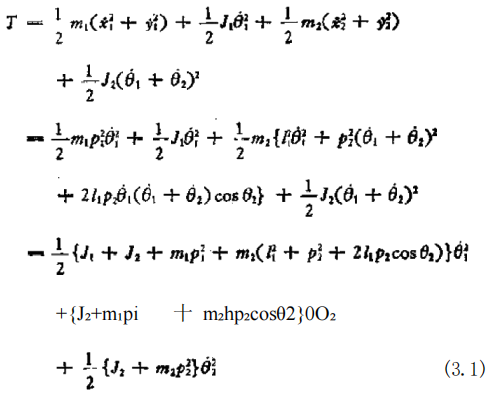
位能U为： U= 加18p₁sin θ₁十 m₂g{1 sin θ₁十 p₂sin(θ₁+θ₂)} (3.2) 由于在力矩,作用下，产生转角80,80 ₂ 时，作了功80 ₁+ M₂80₂,若设 L 一 T 一 U, 则下列拉格朗日 (Lagrange) 方程式成立：

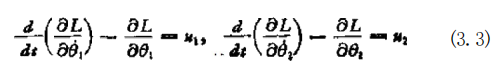
对上式进行计算，得到

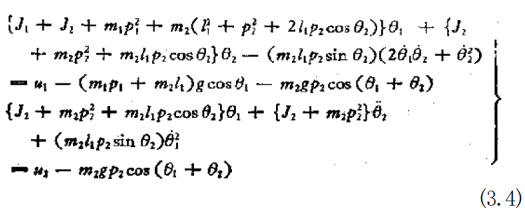
上式可以归结为下列简单表达式： w(0)θ+a(O,0)=+β(0) (3.5)

式中

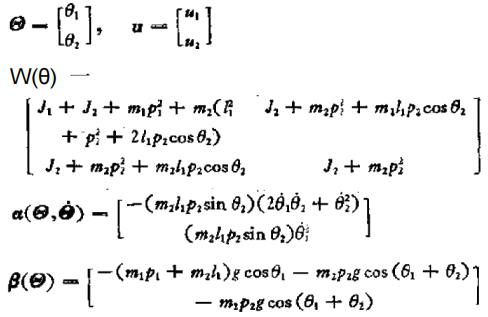
根据(3.5)式，选择0作为变量，这时的运动方程式显然是一个具 有复杂形式的非线性微分方程式。 由(3.1)式还可以清楚地看出，由于 Ow(O)0 是动能7, w(0) 为正定值，所以 w(O) 的逆矩阵通常是存在的，如果用 W(O)- 左乘(3.5)式，则得到 0——W-¹a+W-¹g+W-u 一h(θ,0,u) (3.6) 因为(3.6)式是二阶微分方程式，相对于8=[θ₁,θ₂}',若设x 一 θ,x₂=θ,x 一 θ,xq一θ₁,即设 x=[x₁z₂xjr₄], 则可以得到

下列关系式：

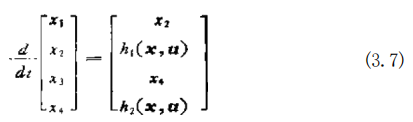
若设(3.7)式右边等于f(x,u), 则(3.7)式变为下列形式：

这和2.1.2节中的(2.20)式是相同的。 对于一般的空间联杆机构，导出的运动方程式通常都可以用 (3.8)式这种形式表示，因此，以后我们将针对(3.8)式讨论控制理 论问题，

3.2.2 控制器的设计 正如在空间联杆机构的运动方程式中看到的那样，控制对象 的动态特性，多数情况下都可以用下列非线性微分方程式表示： x 一 F(x,a),y=Cx (3.9) 现在我们来研究满足(3.9)式的系统控制问题.在未作预先声明 时，假定观测方程y=Cx 中 的 C-I, 即假定y 一 x。 这意味 着系统中的状态变量全都能够观测。 前馈控制 当要求机器人完成某种工作时，通常，机器人每 时每刻的动作都是在动作开始之前预先决定的。这称作轨迹规划 (trajectory planning)。如果规划的轨迹 x(t) 一 x*(t) 可以实现， 则必定存在 u=u*(r), 使得 x*,u* 满足(3.9)式，即必定满足 *=f(x*,u*) (3.10) x* 和 u* 是(3.9)式的解。在不存在干扰的情况下，唯有控制a* 才能够实现 x() 一 x*。因此，采用 u* 的控制叫做前馈控制。 与此对应，如果在(3.9)式中决定的女能使 x 在 x 周围稳 定，则即使存在着干扰，机器人也能在规划轨迹附近工作。 因此， 可以考虑把(3.9)式区分为在 x*,u* 上的运动和在它们周围的运动。 实际状态 x 与 x 往往是有差别的，这种差别△x 可以由 下式确定： x 一 x* 士△x (3.11) 使 △x→0 的控制输入，即使 x 趋于 x* 时的部分控制量△a 可以由下式确定： t 一 u* 十△u (3.12) 将(3.11)式及(3.12)式代入(3.9)式，可以得到 t* 十△i mf(x*十△x,a* 十△t) (3.13) 将(3.13)式按△x,Au 的一次方展开，并且分别与(3.10)式的两边 相减，然后归纳整理△ ,即 t 可 A得 (c △ (参 x (.t )式 a ) (3.14) 在(3.14)式中，如果当△x→0 时能够求得△u, 则(3.10)式 中 的a* 与 该 △u 之和为 u=u*+Aa, 据此，有 x→x*. 这 种关系可以用图3.5表示出来。根据(3.10)式求 u* 的问题，虽然原理上很简单，但是计算量很大，因此，人们研究了各种各样的快 速算法。

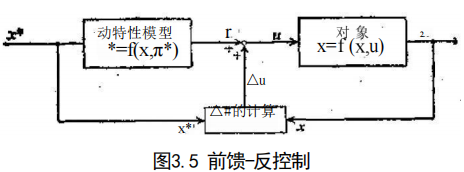
原理上很简单，但是计算量很大，因此，人们研究了各种各样的快 速算法。 此外，在满足△x→0 的情况下求△a, 也是一个困难的问 题。下面我们就来研究这个问题。因为在关于 x 的微分方程式 中，介绍的是当 x→0 时，求 u 的一般方法，所以在关于△x, △a 的微分方程式(3.14)中，希望能适当地以△x 取代 x, 以 △u 取代u,反馈控制 考虑在第二章图2.2中讨论过的例子。为了使问题简单，设 m=r=a=1. 这时水平面上的质点依据运动方 程式 一t 进行运动，当希望这个质点在 x=0 的位置停下来 时，自然需要根据现在的位置x 来决定#的值。例如，考虑设 = 一x时的情况。如果将上述v 值代人运动方程式，则得到 十 x 一 0 (3.15) 这个方程式的解，是围绕 x=0 点的简谐振动，x 在0点是不收敛 的。考虑当设 一 —x—x 时的情况。同样，如果将这个μ代入 运动方程式，则可以得到 无十x 十x=0 (3.16) → 00时，x→0. 正如上述两种情况表明的那样，根据控制对象 的状态x和 交 求x的方法，称为反馈控制，虽然这个例子属于一 种特殊情况，即根据x 和素的线性组合确定,但是它并不排除 可以是*和 x 的非线性函数。 在反馈控制中，包括能使控制对象的状态收敛到0的情况和 不能使状态收敛到0的情况。在反馈控制系统中，我们感兴趣的 是，怎样选择那些能使控制对象的状态收敛到0的系统。 线性反馈控制 选择常系数微分方程式(3.17)表示的系统 (这与第二章(2.27)式(2.28)式是相同的)作为控制对象，考虑一 般的反馈控制问题。 -Ax+Bu,y=Cx (3.17) 为了使问题简单，在上式中设 C=1, 即 设 y 一 x, 现在我们来考 虑，以 u=Fx 这种形式作为反馈控制律的控制问题。 F 称为反 馈增益。因为立是x 的线性组合，所以这种控制称作线性反馈 控制。如果将 a=Fx 代人(3.17)式，则可得到 t=(A+BF)x (3.18) 为了保证(3.18)式的解是渐近稳定的，A+BF 的特征值必须全 都具有负实部(参考2.1.2节)。因此，根据使 A+BF 达到稳定的 条件选择 F, 完全能够保证 x→0. 可是，在(3.17)式中，满足 x→0 的 = Fx 这种形式的 a 可以有很多种，从这些控制中选择哪一种，这是一个重要问题，解决这个问题的一种方法是，规定一个评价函数，然后选择一种能够 使这个评价函数取最小值的 a. 最佳线性反锁控制 给 定 1 的 函 数 x(t),x₂ (:), ·sx(t) 时，考虑泛函 x(t)=[x₁(t),x₂(t)··x(x)]'。 设 , 9 为 标 量 ：

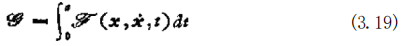
如果 x 的函数形式巳经确定，则(3.19)式的值就确定了。当 x 变化时，9的值也随之变化，使 的值达到最小的 x 可以由变 分法和(3.19)式的下列欧拉(Euler)方程式的解确定。

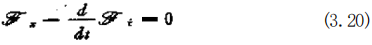
式 中 ， 、 由x,x 的偏微分表示如下：

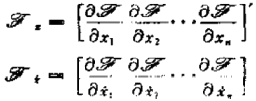
在(3.19)式中，如果x 和元存在着关系s(x,x)=0(s 为向量 函数),那么所需能量是多少呢?因为 s(x,x)=0 是 对 x, 的 约 束条件，所以这时的问题变成为带约束条件的(3.19)式的最小化 问题.在(3.19)式中，增加具有拉格朗日待定乘子λ= ] 的约束条件后，得到

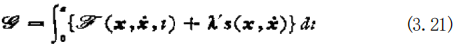
欲求其解 x, 即为求同时满足欧拉方程式(3.22)与约束条件(3.23) 式 的x. (当然，这时可以对(3.22)式的微分进行计算后，与(3.23) 式联立求解)

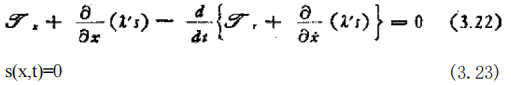
在上述预备知识的基础上，现在举一个典型例子，说明怎样对 评价函数求最小值，并求出满足 x→0 的 u. 最初的例子是

(3.17)式，即对 = Ax+Bt; 以式

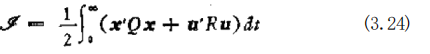
为评价函数，求使评价函数取最小值的 u. 公式(3.24)中的 x'Qx+w'Ra 为二次型形式， Q,R 为 常 数矩阵，当 x≠0,tt 0 时，对于 x,u, 通常满足 x'Qx>0, w'Ru>0 (正定值) ,且 Q,R 为正定矩阵。因为约束条件为 x= Ax 十 Bu, 且考虑到拉格朗日待定乘子，(3.24)式变为

由 于R 为正定对称矩阵，所以存在逆矩阵 R-t, 根据(3.27)式，得 到 u 一 R=¹B'h, 于是根据约束条件 Ax 十Bu 和(3.26)式，并 消 去 α 后 得 到 一 Ax+BR-¹B'λ (3.28) k 一 Qx 一 A'λ (3.29) 这里，我们设联立微分方程式(3.28)和(3.29)的解具有λ= Sx(S 为常数矩阵)这种形式，如果将λ 一.Sx 代人(3.28)式和(3.29) 式，则得 =Ax 十 .BR~³B'Sx (3.30) Sx=Qx—A'Sx (3.31) 如果用S 从左边开始去乘(3.30)式，并且分别减去(3.31)式等式两端，即可消去，得到 {SA+SBR-¹B'S-Q+A'S}x—0 (3.32) 因此如果 SA 十 A'S+SBR*¹B's—Q (3.33)

成立，则满足约束条件元=Ax+Ba 和欧拉方程式(3.26), (3.27)的 x,u 便存在，(3.24)式中的 就可能取得最小值。详 细研究可以断定，在一定条件下，(3. 33)式的解S 不是唯一的，在 式 —R-1B' =R-¹B'Sx (3.34) 中，显然，能使(3.17)式稳定的 u, 的确能使(3.24)式具有最小值。 因为(3.34)式可以写成 u=Fx 这种形式，所以 R-¹B'S 是反馈 增益。方程式(3.33)*被称为黎卡提(Riccati) 方程式。 若已知控制对象的运动方程为 一 # , 评 价 函 数 为 一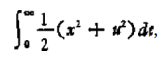

试利用上面讨论的方法确定系统的，因为这 时 4 = 0 ,B=1,R=1,Q-1, 所以黎卡提方程式(3.33)变为 S²—1, 将这些值代人(3.34)式中，得到 一 土x (3.35) 在(3.35)式的解中，能使 一 稳定的1值是 一 一x, 这也正 是使 w Bang-Bang 控 制 满 足 x→0 的 a 的第二个例子，是将 评价函数从(3.24)式变化成下列形式：

式中设 0时的状态 x 为 x 一 xo, 时的状态 x 为 x -0。这时，使(3.36)式具有最小值意味着求一个 u, 使得系统能 从 x=xa 的状态以最短的时间移动到若一0这个状态。这时， 与(3.25)式对应的公式为

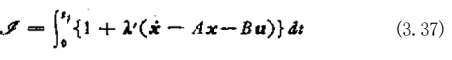
(3.37)式的欧拉方程式为

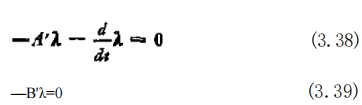
因此，问题变成为求解满足(3.38)式，(3.39)式和约束条件 t 一 Ax+Bu 的 x,λ,u 的问题.但是，不管怎样，欧拉方程式(3.3B) 和(3.39)都意味着没有解存在(λ=0的解无意义)。例如，设水平 面上质点的运动方程式 = u ,因而

与(3.3B)式和(3.39)式对应的公式为

其解为λ₁一₂一0.这说明，如果对控制α不加限制，使用大的 a 总能够迅速达到状态原点。与此对应，是在对 a 有限制的情况 下确定 u 值。从控制α有界的物理意义上去看，对 a 的 限 制 是合理的。 对于评价函数

(3.44)式可以看作是以不加限制的变化的 u 为参数时，h 取最小 值的条件。因此，即使在对 u 附加了限制的情况下，与(3.44)式对 应的条件仍可以认为是以 u 为参数的函数h 取最小值。如果进 行详细分析，同样可以证明这种考虑的正确性。此外，如果根据对 u 的限制，能够找到 的最小值，则 u 的限制范围也就可以找到了，

下面再次对(3 .40)式的例子进行研究。考虑在 |4<1的条 件下，(3.36)式的最短时间问题。对于 x 的欧拉方程式，约束条 件变为

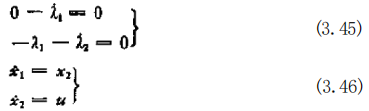
此外，还必须取以“作为参数的下列函数的最小值： h=1-+λ₁(x₁ 一 x₂)+λ₂(x₂ 一 u) (3.47) 因为五为《的一次函数，所以当λ₂ >0时，函数取最小值的条件 为 # = 1 , 当 L₂<0 时，函数取最小值的条件为 x=—1. 若对(3.45)式求解，则得到λ₁=c,λ₂=—ct 十 d(c,d 为 常 数)。所以，可以看出，“是随21符号的变化而最多改变一次符号 的函数。对于 =1, u —1 时的状态点(x₁,x₂), 由 一 x₂, 一 士 1 中 消 去 dr, 得 到 dx₁/dx₂= 土xz, 如果再对此式积分，则 显然得到#1千x2/2=const 的动点轨迹。图3.6表示了这个曲线族。

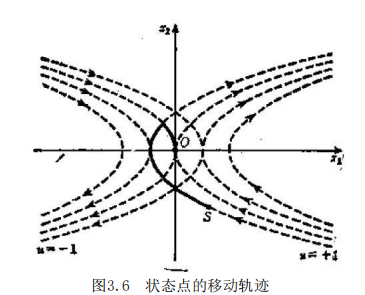
从《最多只改变一次符号和图3.6可以得知，由任意初始状 态 S 以最短时间往O 移动的控制，显然应如图3.6上的粗实线所 示。这样，只使用x 的界限值 一 士1就能够实现最短时间控制，这的确是一件使人很感兴趣的事情。这种控制就称为 Bang-Bang 控制。