传感器算法
利用计算机构成的传感器设备,其优点是可以根据测量得到 的信号,实时的求出有用的信息。这方面的一种最简单的例子,是 对非线性输出传感器的校正。例如,设某器件A 能够产生与力的 平方成比例的电压,当我们利用器件A 测量力时,必须对产生的 电压进行求平方根的运算,这对于计算机来说,是一件很简单的工 作。 此外,就是对于如图2.4所示的所加外力与产生的电压之间 的关系,如果能以数学式子或麦格的形式,将这种关系存贮于计 算机内,就能够根据测得的电压大小,求出相应的力来,这样一来。 如果某器件能够再现输人、输出关系,则即使这种关系很复杂,也 能与计算机结合;获得实用的传感器。
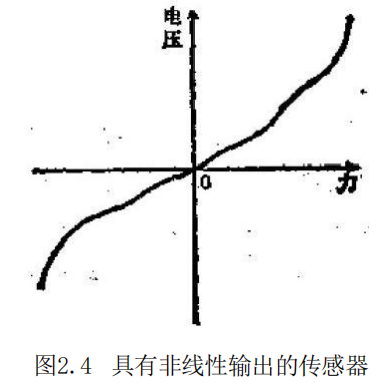
因为在上例中力和电压是——对应的,所以这是一种非常容 易进行测量的例子,但是实际中也存在这样一些复杂的情况,即希 望知道的状态变量比传感器的输出量多。例如对于图2.2中,质 点放在水平面上的例子,想要得到的速度量是不能直接观测到的, 我们希望能从观测到的质点位置中得到它。:即使对于这种情况, 我们也可以通过估计的方法确定状态,下面就介绍这种方法。 卡尔曼-布西(Kalman-Bucy) 的状态估计雍构 现在我们 设状态变量 x 与观测量y 由下式给出;

在上述运算过程中,应用了(2.41),(2.42)和(2.44)式。如果 一 GC 是稳定矩阵,则最终 e→0, 或者说 z→x . 这表明,不管云 的初始值如何,经过足够长的时间后,显然 z 将趋于x 的估计 值。例如,在图2.2的例子中,如果设定G=[g₁gz]', 然后计算 A—GC, 则得

上述理论同样可以推广到离散系统中去。设与(2.41),(2.42)
式对应的离散系统关系式为
x(k)=φx(k—1)+Hu(k—1) (2.47)
y(k)=Cx(k) (2.48)
现在来考虑与(2.44)式对应的下式的估计问题:
z(k)=(① 一 GC)z(k 一 1 ) + Gy(k—1)+Hu(k—1) (2.49)
若设 e(k)=z(k)—x(), 则得 e(})=z(k) 一x(k)
= { ( 一GC)z(k-1)+Gy(k—1)+Ha(k-1)}
—{φx(k—1)+Hu(k—1)}
一(φ一 GC)z(k—1)+GCx(k—1)
一 ①x(k 一 1 )
=(φ—GC)(z(k 一 1 )
一 x(k—1)) 一(φ一 GC)e(k—1) (2.50)
因此,对于满足(①— GC)→0 的 G 矩阵,有 e(k)→0, 从而有 z(k)→x(k), 于是 (t) 给出了 x(k) 的估计值。
卡尔曼-布西的估计结构是一种与(2.41)式的阶次相等的动 态结构。如果应用从(2.42)式得到的信息,虽然可以降低阶次,但 是理论却变得比较复杂了 (Luenberger 观测器).
连续系统滤波器
如上所述,如果利用有关状态转移的 动态特性信息,可以对状态量进行估计。这里,关于动态特性的信息越精确,所得估计便越准确。 然而现实与模型之间的误差 是不可避免的,因此这种误差造成的影响往往也是不容忽视的 。这样一来,由于未能将某些实际因素考虑到模型中去,于是便产生了噪声信号。应该除去的噪声,包括白噪声,频率在90kHz 以上的噪声等。如果知道了什么是噪声,那么就可以从观测数据中除掉噪声信号。下面将以高频分量为噪声的滤波器为例,阐述滤波器理论。
实际中经常采用以y 为 输 入 ,z 为输出的下列常系数线性微分方程表示的滤波器:
z(m十 qz⁰-³ 十 · 十a2 一boy(m十 b₁ym-¹) 十 · ·士bmy
 系数为实数。(2.51)式的一般解是该等式(左 边)=0的一般解与特解之和。这里我们认为(左边)=0的解是 渐近稳定的,(因为这里的目的是要构造一个具有(2.51)式那种 数学表达式形式的滤波器,所以(2.51)式的解不能是发散的,)
系数为实数。(2.51)式的一般解是该等式(左 边)=0的一般解与特解之和。这里我们认为(左边)=0的解是 渐近稳定的,(因为这里的目的是要构造一个具有(2.51)式那种 数学表达式形式的滤波器,所以(2.51)式的解不能是发散的,)
这个条件的实质,首先在于求出 y=aei (式中a、、t均为 实数)时的定常解( → 0时的解).如果取 y, 不的实部,则可以 求得对应于 y=acos ot 的解。取 z=peia 代入(231)式,则得 到下列关系:
{(ico)" 士 a₁(ioo)"-+··· 十 an}βeiol
{b₀(ico)" 士 b₁(iw)=-¹ 十 · ·十bm}aeio (2.52)
对于满足(2.52)式的β,其解为z 一peiot。根据(2.52)式,求输入 与输出之比 z/y=β/a, 则可得到
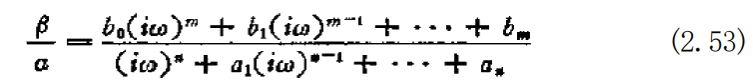
若设 p/α=H(o), 则H 一般为复数,[H(wo)[为输入与输出的振 幅比,argH(o) 表示相位差。如果随着 y =αei 中 的o 变化,输 出的振幅作适当变化,也就是说,如果能够设计出这样一个H(co), 使得对于被看作频率分量的噪声输人,有很小的输出振幅,则 (2.51)式就构成了滤波器。但是,由于对应于0的输人-输出振幅 比 [H(co) | 不便处理,所以在进行设计时,经常采用 [H(o) |²= H(o)E(o)(H 表示共轭复数)这种形式。 巴特沃思(Butterworth)滤波器 (2.54)式代表的巴特沃思 滤波器是一种典型的能滤除高频分量的滤波器例子。(如果改变 (2.54) 式右边的 o, 和 N, 当然可以得到具有各种不同特性的滤 波器。)
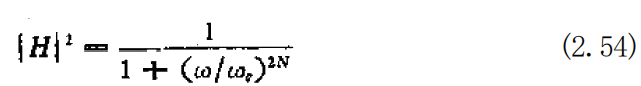
图2.5是(2.54)式的图解表示。在0=0附近的低频段上,输入与 输出的振幅比大体上等于1,而在高频段上,则大体上等于零。在设计具有(2.54)式特性的滤波器 时,需要从(2.54)式中的 [H[² 项求 解H. 但是,表示成(2.53)式那种形 式的H 必须是稳定的。 现在,在(2.54)式中,我们以 N=3,co=1 作为例子,进一步进行计算。
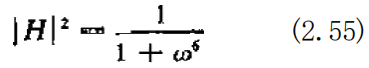
因为在(2.55)式中包含着o 的六次方,所以在H 中将包含0的三次方。为计算该问题,我们选用实数 a₁,Qz₂a₃, 于是可以将(2.55) 式作如下因式分解:
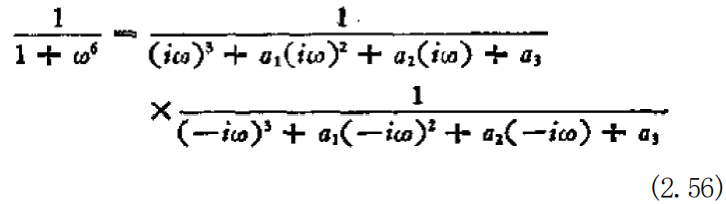
并且H 可以变成为稳定的。在(2.56)式中进行变量代换,即令 io—, 于是有
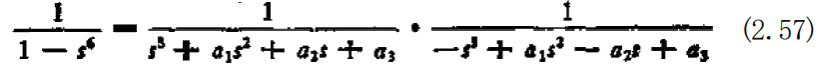
当1 — 5⁶ —(s—1)(s 一 en)(s—2ip)(s+1)(s-e=l³) (s 一5=13)时,镒于滤波器的稳定条件是 x³十 a₁s²+a 十 a₃=0 的解全都具有负实部,又考虑到一γ的共轭复数为一s—?, 显 然H 取下列形式能满足要求:
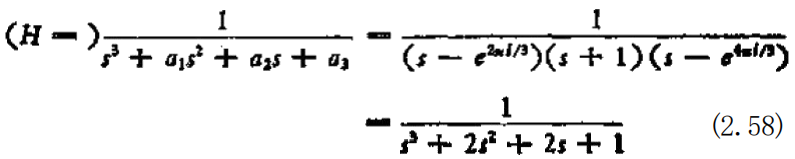
因此,根据(2.51)式,滤波器可以表示为
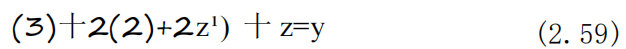
离散系统滤波器现在让我们讨论离散系统滤波器理论, 它与上述连续系统滤波器理论是对应的。与(2.51)式对应的离散 系统差分方程为
z(k)+a₁k(k 一 1 ) 十a₂z(k 二 2 ) 十 十 aaz(k 一 n) 一 bay(k)+b₁y(k—1) 十 · · +bmy(k—m) (2.60)
式中a₁ 到 a,b, 到 b。均为实数,y(k) 和z(k) 分别为第k 次采样 时刻的输入和输出。 若2*十a₁L”¹十 a₂l#-²+ · · ·十 a。=0 的 解的绝对值全都小于1,则(2.60)式是稳定的,该式代表的滤波器 为定常滤波器。滤波器(2.60)式的正弦输人响应特性,可以通过 设 pmgiur, 并以 y(k) 一 ap²,z(k) 一 fpk 代人(2.60)式加以研 究。式中0为输人信号的角频率,T 为采样周期,根据采样定理, 设 toT <π。如 果 将y(k) 一 np*,z(k)=pp² 代入(2.60)式,则得到
(p¹+a₁p-¹ 士 · ·十anpk-#)9 一(bp*+bp-¹ 十 · ·十bp- 加) (2.61) 与(2.53)式对应的输入-输出关系可以用下式表示:
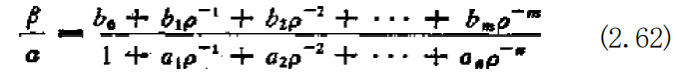
如果设β/c—H(w),H 一般为复数,则|H(o)| 为输入-输出的振 幅 比 ,argH(co) 表示相位差,这与连续系统的情况是相同的。虽 然对于连续系统情况,当给定 (H|² 的形式后,可以确定 H, 但是 对于(2.62)式的情况,由于H 不能构成0的有理函数,因而将使 问题复杂化。因此,通常将采用 tan(oT/2)—w 这种变量变换 的方法,用w 取 代o, 进而确定 H. 经过若干计算,并考虑到 tan(wT/2) 一 w, 显然可以得到下 列关系式:
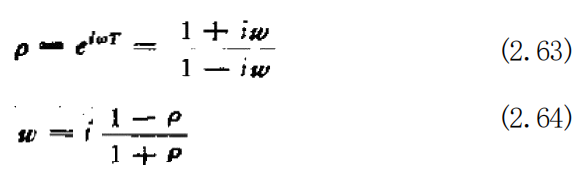
将(2.63)式代入(2.62)式,可以得到关于β/c 的表达式,这时它变 成了w 的有理函数,这个结果是很重要的。此外,(2.62)式的稳定 条件,是将P 看作未知数,并令分母等于零,这时求出的解的绝对 值全都应该小于1.但是,当进行了变量代换,以w 取代了(2.62) 式中的0之后,其稳定条件将是把w 着作未知数,然后令分母等 于零,这时求出的解的虚部应为正值、对以w 表示的H(=/α), 可以从满足
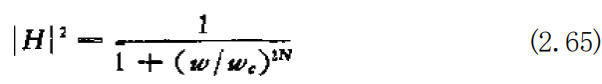
的关系中进行求解(巴特沃思滤波器),与连续系统的情况相同, 若以 w=I,N=3 进行计算,则相应于(2.56)式,有等式
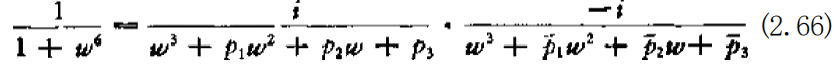
存在,其中1+ w⁵ 一 (w—emió)(w—i)(w—e⁵*i¹4)(w—e⁷*6) ×(w+i)(w-e¹*i/6), 为了保证H 稳定,其条件是H 的极点的虚 部应为正值。如果考虑到w—γ 的共轭复数为w 一宁,则显然可 以得到
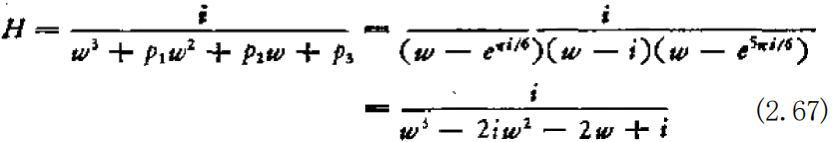
若用(2.64)式置换(2.67)式中的变量,则有
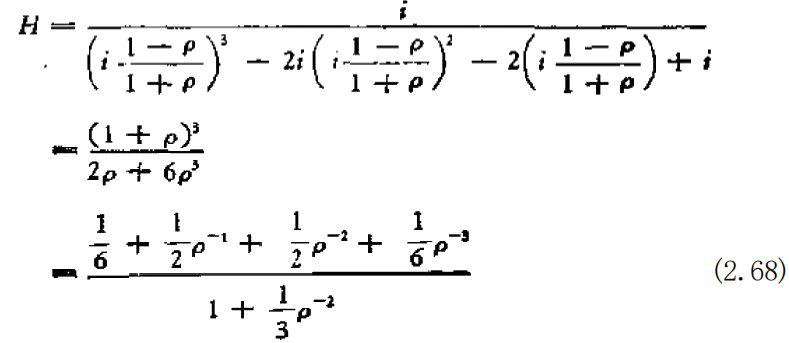
因此,根据(2.62)式,求得的滤波器变为下列形式:
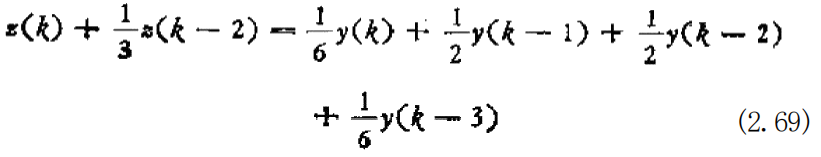
随便看看
- 2024-09-29液压系统冷却器
- 2024-09-18功率-电路基础知识
- 2024-10-29液压系统动密封装置常见故障原因及对策
- 2024-10-01XEM220LC型液压挖掘机的油温过高现象
- 2024-09-14必要工具的介绍-挖掘机点检整备篇
