蒸 本 ( 行 )每服调速翠

如果飞铁在恒定半径的情况下运转，那么飞铁位置的任 何偏移都会使导向阀垂直移动，导致控制区局部地露出控制口，燃油通过这个口流往动力活塞或由动力活塞返回。 飞铁一调速器的弹簧凯构，基本上与前面描述过的机械 调速器相同，不过它小得多，且萸灵敏。 

固定半径的运行具有优越性，因为半径在增益的项目思 并不出现。不过重力比仍很重要，它会减弱调速器弹簧的附度。

由于调速器弹簧的弹力(速度调定)已经给定，重力仅仅在一个精确的速度下使间关闭，稍微偏离这个速度都将使 阀打开，动力活塞将连续移动，改变供油率，直到速度被校 正为止。这是一种和筒单的同步机械调速器类似的同步运 行，这种运行是不大稳定的。为了弄清不稳定的原因(就微 量变化方面而论),作如下分析： 

假设可控流q₁ 与阀门开度 δx 成正比，即Sq!=Cδx. 式中α为阀门流量系数α=δ₁/3x, 并假设活塞移动速率 等于流最变化率，即ADδy=Sq₁, 消去 δg,得到

δy/8z=α/AD (14) 

从机概调速器的基本分所得出8x=Kg·δ①。 

式中Kg 为调速器增益Kg=K₀/(β-R), 

于是对筒单的伺服调速器， 

得到 83/8①=Kgα/A0=-1/vD (13) 

可见是一个带有时间常数t 的积分器。注意：对干同步的机 械调速器，当β=I 时，根据方程式(11),方程式(15)的另 一种形式可写为：

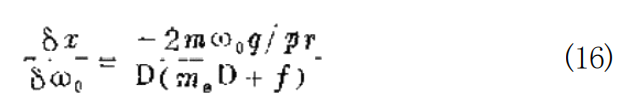
这也是一个积分器。正如从不同观点已得到证期的那 样，在零频率时，这种积分器的特点是其增益为无穷大。 

早在公式(5)中已指出，发动机出近似为一个积分器。

80。/δy=K/ID 

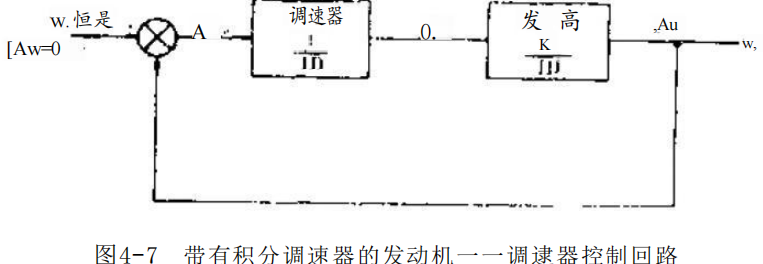
如果将两个积分器联在一个闭环内，如图4-7所示，那 么这个闭环的传递函数，即运动方程式，可从标准教科书中 找到： 

输出/输入=G/(1+G)

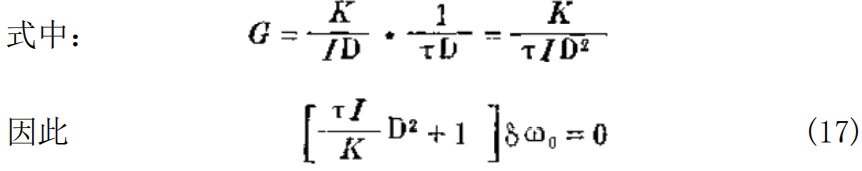
这是一个常系数二阶微分方程，没有D 的一次项，这个 方程的解是一个无阻尼谐波振荡频率：

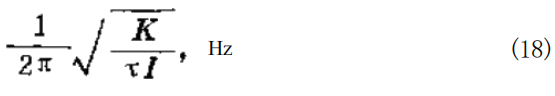
即这种机构的速度将会连续上下振荡。