热传导的基本知识

让我们从一个很简单的情况若手，热流在稳定状态下流过一块平壁的两侧，情况如图3-1所示。

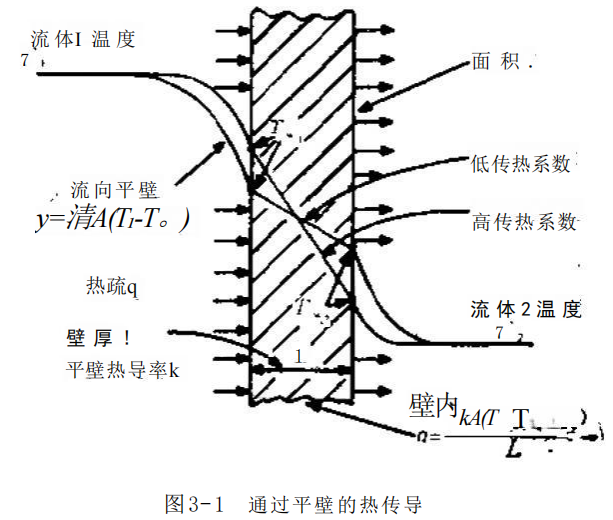
按傅里叶平壁导热方程式：

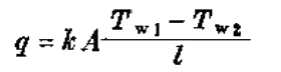
在平壁的任一侧上，牛顿对流换热方程式：

q=h₁A(T₁-Twi)=h₂A(Twz-T₂) 

h₁ 和 h₂ 是在特定的流动条件下平壁两侧的传热系数。 

注意如果h₁ 高，温差(T₁-Tw₁) 将小，反之亦然。因而 壁内温度将依据五；和h₂ 值的大小分布如图3-1所示。

由此得出重要结论：边界条件对导热问题有着决定性的 影响，只有边界条件正确无溪，这个解才是唯一正确的。 

对于二维或三维的稳定状态，情况基本相同。傅里叶方 程式变为：

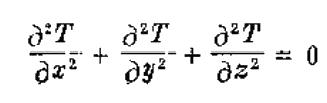
以此同时，给出规定的边界条件就可以得出物体(比如活 寒)内部的温度分布情况。边界条件通常就是规定通过边界 的温度和边界上的传热系数。用有限差或有限单元法或混合 逼近的数值分析法来求解。为此，让算机要大量编码。但 是，要得到正确的答案，必须输入谁确的边界条件，该问题 的解就不成问题了。摆在我们面前的困难是如何鉴别边界条 件的准确性。

对于非稳定问题，相应的微分方程式是：

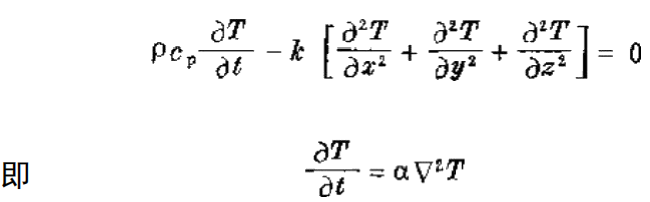
其中α=k/(Pcp) 是导热系数，是导热介质的一种特 性。

方程式(4)的解也是用数值分析法得到的；这种情况下 的边界条件，必须根据空间和时间确定。 

就柴油机来说：一个对流换热的极厚平壁及在平壁一侧 流体温度按周期循环变化时，方程式(4)的分析十分重要， 参考文献(1)的解答，说明热振荡频率越高，它对表面的穿 透能力越小。还有，毕奥系数(=hl/k, 其中无是金属的导 热率，即导热系数)越低，对乎面的热振荡衰减将越多。对 于典型的高速发动机，温度波动的振幅可能只在10℃范围 内，并且.穿透金属的厚度仅只2mm。因此，认为金属内部温 度分布接近稳定状态是有根据的。当然，由于负荷变化引起 的不稳定状态除外，因为这种情况下热振荡频率过低。