发动机的数学模型

图4-1表示了基本的发动机-调速器控制环路。它包括了 一个和调速器刚性连接的载荷诸如发电机。必须注意，发动 机与负荷连接时，若借助于弹性联轴器，将会导致更加复杂 的稳定性问题。这些问题这里将不作讨论。 这个模型里的发动机包括一个燃烧系统，这个燃烧系统 产生扭矩 Gm 作为调速器输出位置y(= 供油齿条位置)的一个函数。

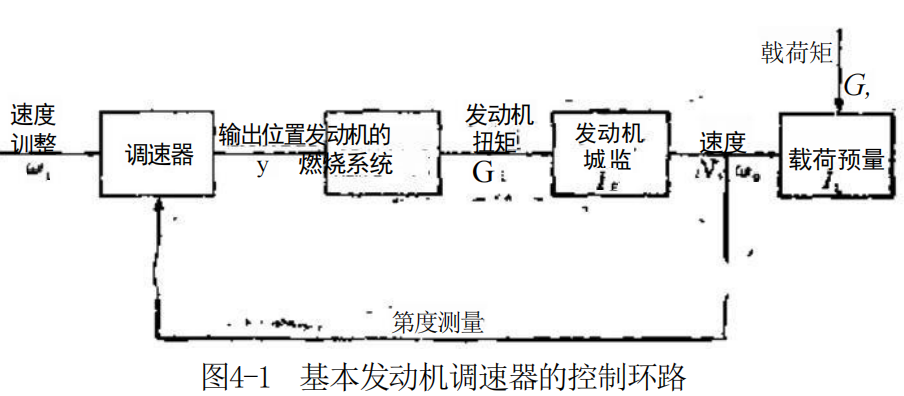
扭矩Gg 为载荷力矩 GL提供条件，Gp 与 GL 之间的任 何差异都会使组合转动惯量(I=Ip+I) 加速或减速。 

从图4-1能看到，发动机，载荷以及调速器全部组成一 个闭合链，形成了一个完整的控制闭环。各个部件的特性对 于确定有效的调节性能起到同样重要的作用，最好的调速器 也不能指望完全控制一个有故障的发动机，这些故障或是调 速器和燃油泵连接松动，或是某个气缸出了毛病，或是调速 器驱动不良，或是其它许多可能产生的故障。 

研究一下图4-2表示的任选发动机和力矩一速度特性。

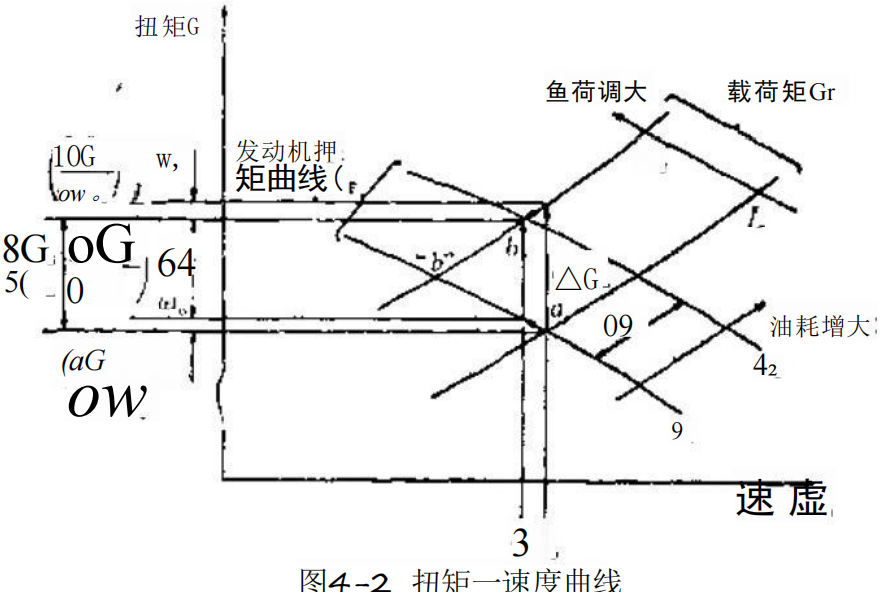
假如施加的载荷产生微量变化△GL (例如船.用螺旋桨 有少量变化)来衡点α发生位移、调节发动机使燃料消耗率 作相应变化84,这样随着速度的微量变化80,产生了一 个新乎衡点“”。

扭矩的最终变化为：

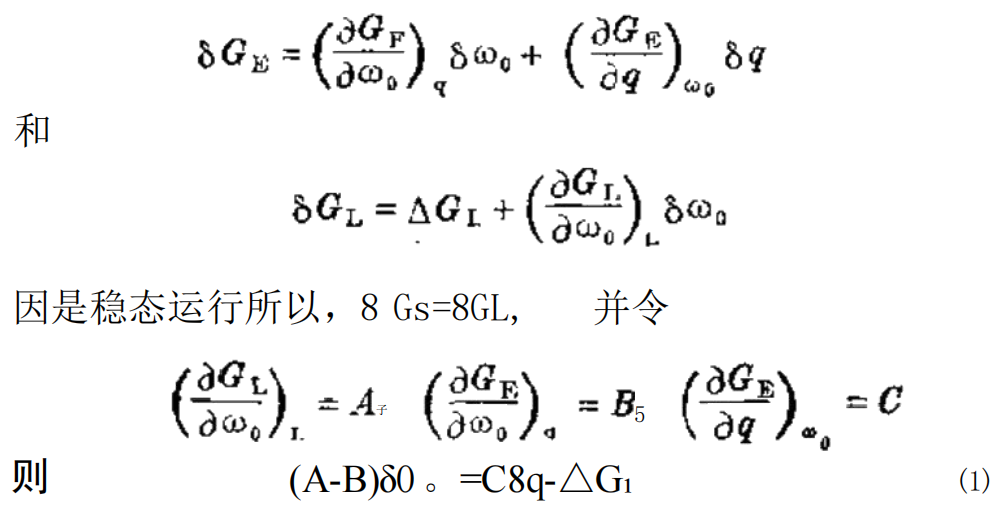
这一公式说明，油耗变化量8q 和载荷变化量△Gz, 使 稳态运行的速度产生变化量80。 如果在不作调节的发动机上油耗率为常数8q=0, 那么:

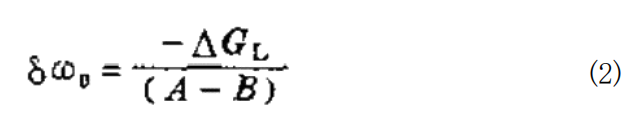
式( 2)表示在载尚增加的情况下，不作调节的发动机将如何 减低速度。在此情况下，在图4-2上新的平衡点应该是 “”。

在带调节的发动机上，油耗率按8q 增加，于是稳态运 行速度的下降变慢了，从而得到

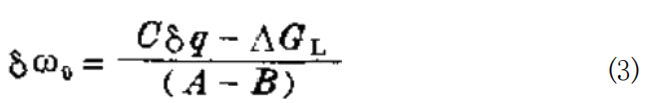
由于采用了调速器，发动机的转速降可以衰减为0,式(3)右 边的分子成为Cδq=△GL, 但这引起了稳定性问题，这在 后面将作讨论。转速降为0的系统称作“同步系统”。

在动力学方面，在平衡点之间的转换过程中，扭矩不平 衡时对转动惯量的速度产生影响。

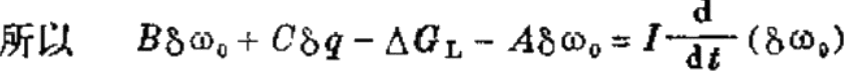
使用微分算子记号D, 即 D=d/dt, 并 令Cδq=Kδy, y 在式中是调速器的输出位置，于是

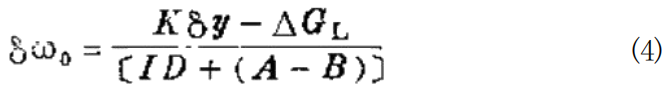
这就是调速发动机转速对载荷的最基本的传递函数”。 

值得注意的是，如果A-B=0、 那么发动机的传递函数简化为

式(5)表明发动机可近似地看成一个积分器。实际上， 只 要 有 供 给 ( 过 量 的 燃 料 ) , 积 分 器 将 继 续 不 断 地 增 加 其 输出(就发动机来说，即增加转速)。运说明在柴油机里 通常B≈0, 如果不进行调节，就有走飞车的倾向。